Selasa, 23 Februari 2021
Senin, 22 Februari 2021
GARIS SINGGUNG PERSEKUTUAN DUA LINGKARAN
Garis singgung lingkaran terdiri dari deretan titik yang tersusun secara berimpit satu sama lain
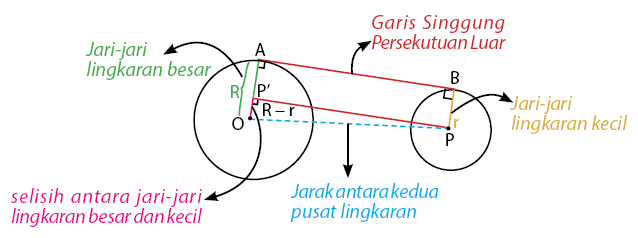
Garis AB adalah garis singgung persekutuan luar dua lingkaran. Konsep untuk mengetahui panjang garis singgung persekutuan luar dua lingkaran adalah teorema pythagoras. Langkah pertama adalah proyeksikan titik P ke garis OA. Panjang garis PP’ sama dengan garis AB, sehingga dengan menghitung panjang PP’ maka kita juga akan mendapatkan panjang AB (garis singgung persekutuan dua lingkaran).
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut.
Karena maka,
Sehingga, rumus garis singgung persekutuan luar dua llingkaran dapat dinyatakan dalam rumus di bawah.
Rumus mencari panjang garis singgung persekutuan luar dua lingkaran:
Keterangan:
AB = PP’ = Garis singgung persekutuan luar lingkaran
OP = Jarak antara kedua pusat lingkaran
R = Jari-jari lingkaran besar
r = jari-jari lingkaran kecil
Dua buah lingkaran memiliki panjang garis singgung persekutuan luar 24 cm dan jarak kedua titik pusat lingkaran 26 cm. Jika panjang jari-jari lingkaran besar 18 cm, maka panjang jari-jari lingkaran yang lain adalah ….
A. 6 cm
B. 8 cm
C. 9 cm
D. 10 cm
Pembahasan:
Berdasarkan data pada soal, kita dapat peroleh gambar di bawah.

Jadi, panjang jari-jari lingkaran yang lain adalah 8 cm.
Garis Singgung Persekutuan Dalam Dua Lingkaran
Seperti halnya garis singgung persekutuan luas dua lingkaran, garis singgung persekutuan dalam dua lingkaran juga melibatkan dua buah lingkaran dan sebuah garis singgung. Bedanya terletak pada posisi garis singgung lingkaran. Dua titik singgung lingkaran pada garis singgung persekutuan luar dua lingkaran terletak di sisi yang sama. Sedangkan dua titik singgung lingkaran pada garis singggung persekutuan dalam dua lingkaran terletak bersebrangan. Untuk lebih jelasnya, perhatikan gambar di bawah!
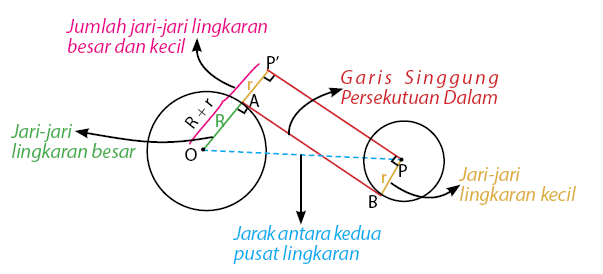
Sama halnya dengan garis singgung persekutuan dalam, garis singgung persekutuan luar juga didapat dengan menerapkan konsep teorema phytagoras.
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut.
Karena maka,
Sehingga, rumus garis singgung persekutuan dalam dua llingkaran dapat dinyatakan dalam rumus di bawah.
Rumus mencari panjang garis singgung persekutuan dalam
Keterangan:
AB = PP’ = Garis singgung persekutuan luar lingkaran
OP = Jarak antara kedua pusat lingkaran
R = Jari-jari lingkaran besar
r = jari-jari lingkaran kecil
Contoh :
Perhatikan gambar berikut!

Panjang jari-jari lingkaran besar dan kecil berturut-turut adalah 10 cm dan 5 cm. Jarak kedua pusat lingkaran adalah 25 cm. Panjang garis singgung AB adalah ….
A. 12 cm
B. 15 cm
C. 17 cm
D. 20 cm
Pembahasan:
Jadi, panjang garis singgung AB adalah 20 cm.
GARIS SINGGUNG PERSEKUTUAN DALAM DUA LINGKARAN
MELUKIS GARIS SINGGUNG PERSEKUTUAN DALAM DUA LINGKARAN
Semoga bermanfaat
Sumber Buku paket Kemendikbud
Selasa, 16 Februari 2021
Senin, 15 Februari 2021
PELATIHAN PEMBUATAN MEDIA PEMBELAJARAN INTERAKTIF MENGGUNAKAN MICROSOFT EXCEL
Pelatihan pembuatan Media pembelajaran interaktif menggunakan Microsoft Excel diadakan tanggal 3-14 Februari 2021
Tujuan
dari pelaksanaan Pelatihan Pembuatan Media Pembelajaran Interaktif Menggunakan Microsoft Excel adalah agar para guru dapat memanfaatkan kesempatan untuk mengembangkan diri secara optimal tentang pembuatan media
pembelajaran interaktif dengan microsoft excel,sebagai modal dalam mengimplementasikan pembelajaran kepada siswa dan
khususnya
a.
Guru dapat memperoleh pemahaman dan keterampilan dalam membuat dan
membagi panel.
b.
Guru dapat memperoleh pemahaman dan keterampilan dalam mengcopy sheet dan
membuat hyperlink.
c.
Guru dapat memperoleh pemahaman dan
ketrampilan dalam mengisi mataeri dan membuat soal evaluasi.
d.
Guru dapat memperoleh pemahaman dan
ketrampilan dalam membuat background dan cover media
e.
Guru dapat memperoleh pemahaman dan keterampilan dalam memprotek media
Pelatihan
dilakukan secara daring lewat telegram, materi disajikan dalam bentuk video dan
pdf
Produk hasil pelatihan langsung diujicobakan
pada para siswa
Terimakasih telah diizinkan mengikuti pelatihan sehingga bisa membuat media pembelajaran untuk siswa
Terimakasih banyak ilmunya Pak Marjito, S..Pd
BANGUN RUANG SISI DATAR(BALOK)
Ciri-Ciri Balok
Perhatikan gambar balok di bawah ini.

Berdasarkan gambar di atas diperoleh informasi bahwa balok memiliki ciri-ciri sebagai berikut :
- Memiliki 8 buah titik sudut, yaitu titik A, B, C, D, E, F, G, dan H
- Memiliki 6 buah sisi berbentuk persegi panjang, yaitu sisi ABCD, EFGH, ABFE, DCGH, BCGF, dan ADHE
- Memiliki 12 buah rusuk, yaitu AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan DH
- Memiliki 12 buah diagonal sisi, yaitu AF, BE, BG, CF, CH, DG, AH, DE, EG, FH, AC, dan BD
- Memiliki 4 buah diagonal ruang, yaitu AG, EC, BH, dan FD
Luas Permukaan Balok
Perhatikan gambar balok berikut ini.
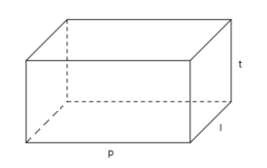
Permukaan sebuah balok terdiri atas 6 buah persegi panjang, sehingga luas permukaan sebuah balok sama dengan jumlah luas keenam persegi panjang tersebut.
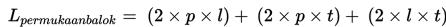
Contoh :
Sebuah kotak permen berbentuk balok berukuran panjang 10 cm, lebar 5 cm, dan tinggi 6 cm.
Luas permukaan kotak permen
= (2 x p x l) + (2 x p x t) + (2 x l x t)
= (2 x 10 x 5) + (2 x 10 x 6) + (2 x 5 x 6)
= 100 + 120 + 60
= 280 cm2
Volum Balok
Perhatikan gambar balok berikut ini.
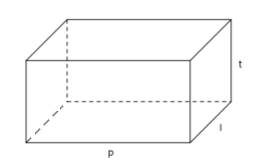
Volum sebuah balok dengan panjang p, lebar l, dan tinggi t dapat ditentukan menggunakan rumus sebagai berikut :
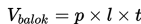
Contoh :
Pada permasalahan yang dihadapi oleh Andika, diketahui bahwa bak mandi di rumah Andika berbentuk balok dengan panjang 2 meter, lebar 1 meter, dan tinggi satu meter.
Volum bak mandi
= volum balok
= p x l x t
= 2 x 1 x 1
= 2 m3
= 2.000 dm3
= 2.000 liter
Karena satu buah ember mampu menampung 10 liter air, maka untuk memenuhi bak mandi tersebut Andika harus mangangkut ember tersebut sebanyak = 2.000 : 10 = 200 kali.
Rabu, 10 Februari 2021
BANGUN RUANG SISI DATAR(KUBUS)
Ciri-Ciri Kubus
Perhatikan gambar kubus di bawah ini.
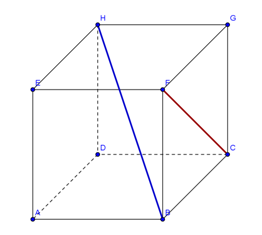
Berdasarkan gambar di atas diperoleh informasi bahwa kubus memiliki ciri-ciri sebagai berikut :
- Memiliki 8 buah titik sudut, yaitu titik A, B, C, D, E, F, G, dan H
- Memiliki 6 buah sisi berbentuk persegi yang kongruen, yaitu sisi ABCD, EFGH, ABFE, DCGH, BCGF, dan ADHE
- Memiliki 12 buah rusuk, yaitu AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan DH
- Memiliki 12 buah diagonal sisi, yaitu AF, BE, BG, CF, CH, DG, AH, DE, EG, FH, AC, dan BD
- Memiliki 4 buah diagonal ruang, yaitu AG, EC, BH, dan FD
Beberapa hari lagi adik Rima akan berulang tahun. Rima telah menyiapkan sebuah hadiah dalam kotak berbentuk kubus dengan ukuran rusuk 30 cm. Ia kemudian pergi ke toko membeli sebuah kertas kado. Kertas kado tersebut berbentuk persegi berukuran 60 cm x 60 cm. Risma ragu apakah kertas tersebut cukup atau tidak untuk membungkus hadiah miliknya, karena ia tidak membawa hadiah tersebut ke toko.
Menurut kalian, apa yang dapat dilakukan Risma untuk memperkirakan apakah kertas tersebut cukup atau tidak? Mari temukan jawabannya dalam topik kali ini.
Luas Permukaan Kubus
Perhatikan gambar kubus berikut ini.
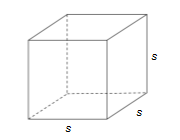
Permukaan sebuah kubus terdiri atas 6 buah persegi yang kongruen, sehingga luas permukaan sebuah kubus sama dengan jumlah luas keenam persegi tersebut.
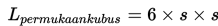
Mari kita selesaiakan permasalahan yang dihadapi oleh Risma
Pada permasalahan yang dihadapi oleh Risma,
- Luas permukaan hadiah = Luas permukaan kubus = 6 x 30 x 30 = 5.400 cm2
- Luas kertas kado = 60 x 60 = 3.600 cm2
Karena luas kertas kado kurang dari luas permukaan hadiah, berarti kertas kado tersebut tidak cukup untuk membungkus hadiah tersebut.
Dengan demikian, Risma harus membeli lebih dari satu kertas kado untuk dapat membungkus hadiah untuk adiknya.
Volum Kubus
Perhatikan gambar kubus berikut ini.

Volum sebuah kubus dengan rusuk s dapat ditentukan dengan rumus berikut ini :
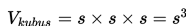
Contoh :
Sebuah akuarium berbentuk kubus dengan panjang rusuk 30 cm. Berapa literkah air yang diperlukan untuk memenuhi akuarium tersebut?
Jawab :
Untuk menentukan banyaknya air yang dapat digunakan untuk memenuhi akuarium, kita harus menentukan volum dari akuarium tersebut.
Volum akuarium
= volum kubus
= s x s x s
= 30 x 30 x 30
= 9.000 cm3
= 9 dm3
= 9 liter










