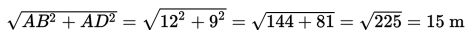Pythagoras merupakan seorang ahli filsafat dan matematika dari Yunani.
Beliau hidup antara tahun 569 – 475 SM.
Salah satu pernyataan yang pernah diungkapkan oleh Pythagoras selama hidupnya adalah bahwa “kuadrat sisi miring suatu segitiga siku-siku sama dengan jumlah kuadrat sisi-sisi yang lain”.
Pernyataan inilah yang kemudian dikenal sebagai Teorema Pythagoras.
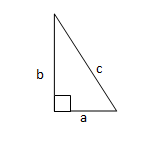
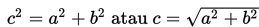
Berdasarkan rumus umum tersebut, kita dapat menentukan panjang sisi-sisi lain dari segitiga siku-siku tersebut menggunakan rumus sebagai berikut :

Contoh :
Tentukan panjang sisi miring segitiga siku-siku berikut ini.
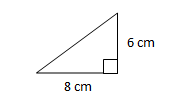
Jawab :
Misal : a = 6 cm dan b = 8 cm
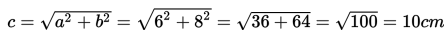
Tripel Pythagoras
Jika a, b, c adalah tiga buah bilangan asli dimana kuadrat bilangan terbesar sama dengan jumlah kuadrat bilangan-bilangan lainnya, maka bilangan a, b. c disebut tripel Pythagoras.
Contoh :
Bilangan 6, 8, 10 merupakan tripel Pythagoras karena 102 = 62 + 82
Teorema Pythagoras dalam Segitiga Istimewa
Perhatikan gambar berikut ini :
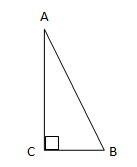
Pada segitiga siku-siku ABC dimana ∠A = 300 dan ∠B = 600, berlaku :
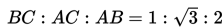
Contoh :
Pada segitiga siku-siku ABC di atas berlaku BC : AC : AB = 1 : √3 : 2.
Jika panjang BC = 3 cm maka, AC = √3 x 3 = 3√3 cm dan AB= 2 x 3 = 6 cm.
Berikutnya, perhatikan segitiga berikut ini :

Pada segitiga siku-siku PQR dimana ∠P = 450 dan ∠Q = 450, berlaku :
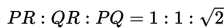
Contoh :
Pada segitiga siku-siku PQR di atas berlaku PR : QR : PQ = 1 : 1 : √2
Jika panjang PR adalah 7 cm, maka PQ = √2 x 7 = 7√2 cm
Pak Rudi memiliki sebidang tanah berbentuk persegi panjang dengan ukuran panjang 12 meter dan lebar 9 meter. Masing-masing sebuah pasak ditancapkan pada sudut-sudut tanah tersebut.
Pak Rudi kemudian mengikat sebuah tali pada satu pasak dan menghubungkannya dengan pasak yang lain hingga membentuk diagonal pada sebidang tanah tersebut.
Menurut kalian, berapa panjang tali minimal yang dibutuhkan Pak Rudi?
Permasalahan yang dihadapi Pak Rudi dapat dilukiskan dengan gambar berikut ini.
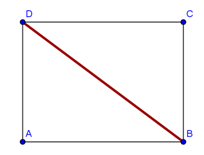
Diketahui : panjang tanah = AB = 12 m dan lebar tanah = AD = 9 m.
Panjang tali yang dibutuhkan Pak Rudi = BD =