Perbandingan
adalah suatu cara untuk membandingkan dua nilai atau lebih dari suatu besaran
yang sama.
Perbandingan banyak ditemukan dalam kehidupan sehari-hari, misalnya: Perbandingan usia ayah dan anak, perbandingan tinggi, perbandingan berat badan, dan lainnya. Perbandingan biasanya dinyatakan dengan simbol ( : )
Perbandingan banyak ditemukan dalam kehidupan sehari-hari, misalnya: Perbandingan usia ayah dan anak, perbandingan tinggi, perbandingan berat badan, dan lainnya. Perbandingan biasanya dinyatakan dengan simbol ( : )
Sebagai
ilustrasi perhatikan contoh berikut :
a. Usia Ayah 45 tahun dan usia ibu 40 tahun, sedangkan usia Ali 15 tahun serta usia Ani 10 tahun.
a. Usia Ayah 45 tahun dan usia ibu 40 tahun, sedangkan usia Ali 15 tahun serta usia Ani 10 tahun.
Perbandingan
usia ayah dan ibu = 45 tahun : 40 tahun = 45 : 40 = 9 : 8
Perbandingan Usia Ali dan Ani = 15 tahun : 10 tahun = 15 : 10 = 3 : 2
Perbandingan usia Ayah dan Ali = 45 tahun : 15 tahun = 45 : 15 = 3 : 1
Perbandingan Usia Ali dan Ani = 15 tahun : 10 tahun = 15 : 10 = 3 : 2
Perbandingan usia Ayah dan Ali = 45 tahun : 15 tahun = 45 : 15 = 3 : 1
Cara menyederhana kan perbandingan:
1. Pada perbandingan antara
besaran yang berbeda, bisa diubah keduanya ke jenis satuan terkecil.
2. Kedua sisi dibagi dengan
nilai yang sama, sampai keduanya tidak bisa dibagi lagi.
3. Atau bagikan kedua sisi dengan Faktor
Persekutuan Terbesar (FPB) dari kedua sisi.
Skala
Istilah skala sering kita
jumpai kalau kita membuka peta/atlas.
Jika pada peta tertulis
skala 1 : 5.000.000, berarti :
1 cm pada peta mewakili 5.000.000 cm jarak yang sebenarnya, atau
1 cm pada peta mewakili 50.000 m jarak yang sebenarnya, atau
1 cm pada peta mewakili 50 km jarak yang sebenarnya
Skala adalah perbandingan ukuran pada gambar (cm) dengan ukuran sebenarnya (cm) Tampak bahwa skala menggunakan satuan cm untuk dua besaran yang dibandingkan Perlu diingat bahwa : 1 km = 1.000 m = 100.000 cm.
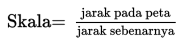
Rumus Jarak pada peta:
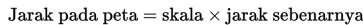
Rumus Jarak sebenarnya:
 Contoh berikut menjelaskan bagaimana kita menggunakan skala pada sebuah peta.
Contoh berikut menjelaskan bagaimana kita menggunakan skala pada sebuah peta.
1 cm pada peta mewakili 5.000.000 cm jarak yang sebenarnya, atau
1 cm pada peta mewakili 50.000 m jarak yang sebenarnya, atau
1 cm pada peta mewakili 50 km jarak yang sebenarnya
Skala adalah perbandingan ukuran pada gambar (cm) dengan ukuran sebenarnya (cm) Tampak bahwa skala menggunakan satuan cm untuk dua besaran yang dibandingkan Perlu diingat bahwa : 1 km = 1.000 m = 100.000 cm.
Rumus Skala:
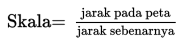
Rumus Jarak pada peta:
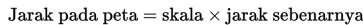
Rumus Jarak sebenarnya:

a. Pada sebuah peta jarak tempat A dan B adalah 3 cm, padahal
jarak A dan B sebenarnya 450 km.
Tentukan skala yang dipergunakan pada peta tersebut !
Tentukan skala yang dipergunakan pada peta tersebut !
Jawab :
Skala = Ukuran pada peta : Ukuran yang sebenarnya
= 3 cm : 450 km
= 3 cm : 45.000.000 cm (pada skala harus menggunakan satuan cm)
= 3 : 45.000.000
= 1 : 15.000.000
Skala = Ukuran pada peta : Ukuran yang sebenarnya
= 3 cm : 450 km
= 3 cm : 45.000.000 cm (pada skala harus menggunakan satuan cm)
= 3 : 45.000.000
= 1 : 15.000.000
b. Pada sebuah peta jarak kota A ke kota B adalah 8 cm. Jika
skala peta itu adalah 1 : 500.000, maka berapakah jarak sebenarnya kedua kota
tersebut ?
Jawab :
Skala 1 = 500.000 berarti 1 cm pada peta mewakili jarak 500.000 cm jarak sesungguhnya, atau 1 cm pada peta mewakili jarak 5 km jarak sesungguhnya.
Skala 1 = 500.000 berarti 1 cm pada peta mewakili jarak 500.000 cm jarak sesungguhnya, atau 1 cm pada peta mewakili jarak 5 km jarak sesungguhnya.
c. Sebuah peta menggunakan skala 1 : 25.000.000 . Jika jarak dua
tempat sebenarnya 300 km, berapakah jarak kedua tempat itu pada peta ?
Jawab :
Skala 1 : 25.000.000
Artinya 1 cm pada peta mewakili 25.000.000 cm jarak sesungguhnya, atau 1 cm pada peta mewakili 250 km jarak sesungguhnya.
Jadi jarak kedua tempat itu pada peta adalah 300 : 250 = 1,2 cm
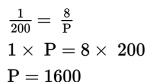
Lebar rumah sebenarnya dapat ditentukan sebagai berikut:

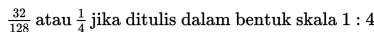
Skala 1 : 25.000.000
Artinya 1 cm pada peta mewakili 25.000.000 cm jarak sesungguhnya, atau 1 cm pada peta mewakili 250 km jarak sesungguhnya.
Jadi jarak kedua tempat itu pada peta adalah 300 : 250 = 1,2 cm
Suatu maket perumahan dibuat dengan skala 1: 200. Ukuran setiap rumah dalam tersebut adalah 8cm × 4cm.
a. Hitunglah panjang dan lebar rumah sebenarnya
b. Perbandingan luas rumah pada maket dengan luas sebenarnya
a. Hitunglah panjang dan lebar rumah sebenarnya
b. Perbandingan luas rumah pada maket dengan luas sebenarnya
Penyelesaian:
a. Skala maket 1 : 200
Panjang rumah pada maket = 8cm
Lebar rumah pada maket = 4cm
Panjang rumah pada maket = 8cm
Lebar rumah pada maket = 4cm
Misalkan P adalah panjang rumah sebenarnya dan L adalah lebar rumah sebenarnya, sehingga panjang rumah sebenarnya dapat ditentukan dengan menggunakan prinsip perbandingan berikut:
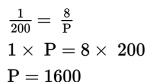
Jadi, panjang rumah sebenarnya adalah 1600cm atau 16m.
Lebar rumah sebenarnya dapat ditentukan sebagai berikut:

b. Luas rumah pada maket = 8cm × 4cm = 32cm2
Luas rumah sebenarnya = 16m × 8m = 128m2
Luas rumah sebenarnya = 16m × 8m = 128m2
Jadi, perbandingan luas rumah pada maket dengan luas rumah sebenarnya adalah:
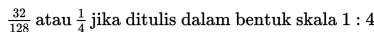
Jenis Perbandingan
a.
Perbandingan Senilai
Perbandingan
senilai berkaitan dengan perbandingan dua buah besaran, di mana jika besaran
yang satu berubah naik/turun, maka besaran yang lain juga berubah naik/turun.
Contoh masalah yang berkaitan dengan perbandingan senilai adalah :
Contoh masalah yang berkaitan dengan perbandingan senilai adalah :
o Jumlah
barang yang dibeli dengan harga yang harus di bayar
o Jumlah
konsumsi bahan bakar dan jarak yang ditempuh
o Jumlah
kaleng cat dan luas permukaan yang bisa di cat
Cara menyelesaikan masalah perbandingan senilai adalah dengan :
a. Menentukan nilai satuan
Dilakukan dengan menentukan nilai satuan dari besaran yang dibandingkan, baru kemudian dikalikan dengan besaran yang ditanyakan.
b. Menuliskan perbandingan senilai
Dilakukan dengan perbandingan langsung antara dua keadaan atau lebih
a. Menentukan nilai satuan
Dilakukan dengan menentukan nilai satuan dari besaran yang dibandingkan, baru kemudian dikalikan dengan besaran yang ditanyakan.
b. Menuliskan perbandingan senilai
Dilakukan dengan perbandingan langsung antara dua keadaan atau lebih
b.
Perbandingan Berbalik Nilai
Perbandingan
berbalik nilai berkaitan dengan membandingkan dua buah keadaan di mana jika
besaran yang satu bertambah/berkurang maka besaran yang lain
berkurang/bertambah.
Masalah yang berkaitan dengan perbandingan berbalik nilai antara lain :
Masalah yang berkaitan dengan perbandingan berbalik nilai antara lain :
o Banyaknya
pekerja dengan waktu yang diperlukan untuk menyelesaikan pekerjaan (untuk
pekerjaan yang sama)
o Kecepatan
dengan waktu tempuh (untuk jarak yang sama)
o Banyaknya
ternak dan waktu untuk menghabiskan makanan tersebut (untuk jumlah makanan
ternak yang sama)
Lebih lengkapnya pelajari yang di bawah ini
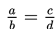


Data pada tabel di atas dapat disajikan pada koordinat kartesius seperti di bawah ini:
Dari data pada tabel dan grafik, kalian dapat mengambil kesimpulan bahwa:

Proporsi yang berlaku pada baris ke-1 dan ke-3 adalah

2. Perbandingan berbalik nilai
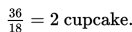
a. Jika tamu yang hadir 12, maka cupcake yang diterima tamu =
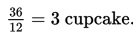
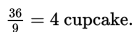
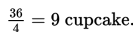
Data tersebut dapat disajikan pada tabel berikut ini:
Data pada tabel 2 dapat disajikan pada koordinat kartesius seperti di bawah ini:


Contoh:

Contoh:

perbandingan senilai
Lebih lengkapnya pelajari yang di bawah ini
ada topik kali ini kalian akan mempelajari tentang menyelesaikan masalah - masalah dalam kehidupan nyata yang berkaitan dengan proporsi.
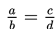
adalah suatu proporsi jika dan hanya jika ad = bc.
Marilah kita pelajari bagaimana menyelesaikan masalah proporsi dengan bantuan tabel dan grafik.
1. Perbandingan senilai
Ciri permasalahan yang berkaitan dengan perbandingan senilai dapat kalian lihat dari contoh berikut ini.
Ciri permasalahan yang berkaitan dengan perbandingan senilai dapat kalian lihat dari contoh berikut ini.
Contoh:
Seorang pedagang membeli 25 karung yang berisikan semangka dengan total berat 3 kuintal. Setelah semua semangka dihitung ternyata terdapat 150 semangka. Berapakah berat semangka yang dibeli pedagang jika:
a. pedagang hanya membeli 42 semangka yang besarnya sama.
b. pedagang hanya membeli 120 semangka semangka yang besarnya sama.
a. pedagang hanya membeli 42 semangka yang besarnya sama.
b. pedagang hanya membeli 120 semangka semangka yang besarnya sama.
Jawab:
Dari soal di atas pedagang membeli 300kg semangka (3 kuintal = 300kg) dan mendapat 150 semangka.
Dari soal di atas pedagang membeli 300kg semangka (3 kuintal = 300kg) dan mendapat 150 semangka.

a. Jika pedagang hanya membeli 42 semangka maka beratnya adalah 42 × 2 kg = 84 kg
b. Jika pedagang hanya membeli 120 semangka maka beratnya adalah 120 × 2 kg = 240 kg
b. Jika pedagang hanya membeli 120 semangka maka beratnya adalah 120 × 2 kg = 240 kg
Data banyak semangka dan beratnya dapat disajikan dalam tabel 1 berikut ini:

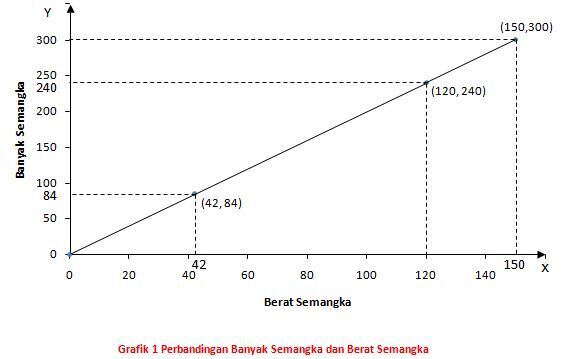
Data pada tabel di atas dapat disajikan pada koordinat kartesius seperti di bawah ini:

Dari data pada tabel dan grafik, kalian dapat mengambil kesimpulan bahwa:
1) Pada tabel 1, semakin banyak buah semangka yang dibeli, maka semakin bertambah beratnya. Semakin sedikit buah semangka yang dibeli maka semakin berkurang beratnya.
2) Coba kalian perhatikan tabel 1, kemudian perhatikan baris ke-1 dan baris ke-3;

Ternyata perbandingan banyak semangka pada baris ke-1 dan ke-3 senilai dengan perbandingan berat semangka pada baris tersebut.
Demikianlah seterusnya untuk perbandingan dua baris yang berbeda. Perbandingan dengan ciri seperti itu disebut dengan perbandingan senilai.
Proporsi yang berlaku pada baris ke-1 dan ke-3 adalah

3) Jika ditarik kurva yang melalui pasangan titik perbandingan, maka kurva tersebut berupa garis lurus.
2. Perbandingan berbalik nilai
Ciri permasalahan yang berkaitan dengan perbandingan berbalik nilai dapat kalian lihat dari contoh berikut ini.
Contoh:
Ibu menyediakan 3 dosin cupcake untuk acara arisan keluarga. Undangan telah disebarkan untuk 18 tamu undangan. Berapakah banyak cupecake yang diterima tamu jika cupcake dibagi rata untuk setiap tamunya?
a. apabila ternyata tamu yang hadir adalah 12 tamu.
b. apabila ternyata tamu yang hadir adalah 9 tamu.
c. apabila ternyata tamu yang hadir adalah 4 tamu.
a. apabila ternyata tamu yang hadir adalah 12 tamu.
b. apabila ternyata tamu yang hadir adalah 9 tamu.
c. apabila ternyata tamu yang hadir adalah 4 tamu.
Jawab:
Dari soal di atas kita ketahui bahwa berapapun tamu yang akan hadir, ibu hanya mempersiapkan 3 dosin cupcake. Total cupcake yang disediakan adalah 3 × 12 = 36 cupcake.
- Dengan demikian jika semua tamu hadir maka cupcake yang diterima setiap tamu =
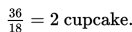
a. Jika tamu yang hadir 12, maka cupcake yang diterima tamu =
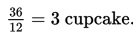
b. Jika tamu yang hadir 9, maka cupcake yang diterima tamu =
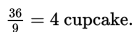
c. Jika tamu yang hadir 4, maka cupcake yang diterima tamu =
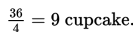
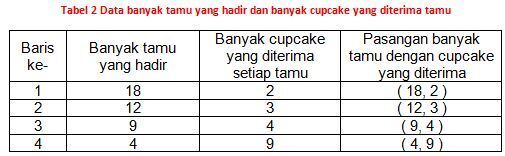
Data tersebut dapat disajikan pada tabel berikut ini:

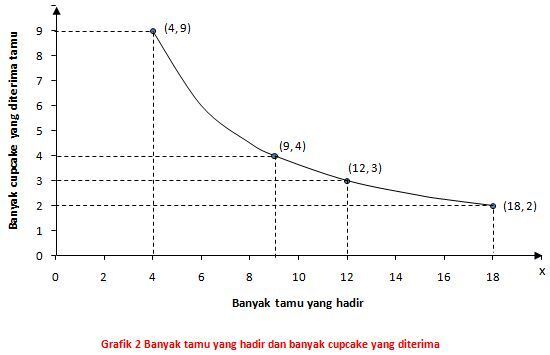
Data pada tabel 2 dapat disajikan pada koordinat kartesius seperti di bawah ini:

Dari data pada tabel 2 dan grafik 2, kalian dapat mengambil kesimpulan bahwa:
1) Pada tabel 2, semakin banyak tamu yang hadir, maka semakin sedikit jatah cupcake yang diterima tamu.
2) Coba kalian perhatikan tabel 2 kemudian perhatikan baris ke-1 dan baris ke-2;
2) Coba kalian perhatikan tabel 2 kemudian perhatikan baris ke-1 dan baris ke-2;

Ternyata perbandingan banyak tamu pada baris ke-1 dan ke-2 berkebalikan dengan perbandingan banyak cupcake pada baris tersebut. Demikianlah seterusnya untuk perbandingan dua baris yang lain. Perbandingan dengan ciri seperti itu disebut dengan perbandingan berbalik nilai.
Proporsi yang berlaku pada baris ke-1 dan ke-2 adalah

3) Jika ditarik kurva yang melalui pasangan titik perbandingan, maka kurva tersebut berupa garis lengkung.
Contoh:
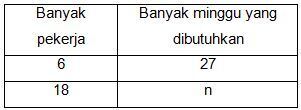
Sebuah proyek pembuatan jembatan memerlukan 6 pekerja untuk menyelesaikan proyek tersebut dalam waktu 27 minggu. Berapa hari yang diperlukan untuk menyelesaikan jembatan apabila pekerja ditambah 12 orang pekerja?
Jawab:
Soal tersebut merupakan soal proporsi berupa perbandingan berbalik nilai karena semakin banyak pekerja maka semakin sedikit waktu yang digunakan untuk menyelesaikan proyek jembatan.
Total pekerja menjadi 6 + 12 = 18 pekerja. Misalkan n adalah banyak minggu yang dibutuhkan oleh 18 orang pekerja.
Total pekerja menjadi 6 + 12 = 18 pekerja. Misalkan n adalah banyak minggu yang dibutuhkan oleh 18 orang pekerja.
Apabila data disajikan dalam tabel menjadi sebagai berikut:


n = 9 minggu = 9 minggu × 7 = 63 hari
Banyak hari yang dibutuhkan oleh 18 pekerja adalah 63 hari.
Banyak hari yang dibutuhkan oleh 18 pekerja adalah 63 hari.
Contoh:
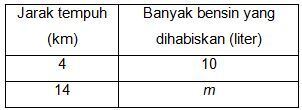
Ayah menghabiskan bensin sebanyak 10 liter untuk menempuh perjalanan ke luar kota sejauh 4 kilometer. Berapakah bensin yang dibutuhkan ayah jika ayah menempuh perjalanan sejauh 14 kilometer?
Jawab:
Soal tersebut merupakan soal proporsi berupa perbandingan senilai karena semakin jauh jarak tempuh ayah, akan semakin banyak bensin yang ia habiskan. Misalkan m adalah banyak bensin yang dihabiskan saat menempuh jarak 14 km. Bila data disajikan pada sebuah tabel menjadi:


Jadi, bensin yang dibutuhkan ayah untuk menempuh jarak 14 kilometer adalah sebanyak 35 liter.
