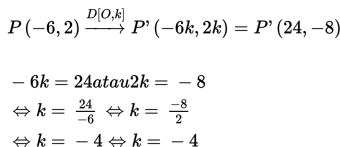Untuk persiapan Ujian Sekolah silahkan dipelajari video berikut..
Sabtu, 14 Januari 2023
Sabtu, 20 Oktober 2018
BANGUN RUANG SISI LENGKUNG
Pengertian Bangun Ruang
Sisi Lengkung
Bangun ruang sisi lengkung adalah kelompok bangun ruang
yang memiliki bagian-bagian yang berbentuk lengkungan. Biasanya bangun ruang
ini memiliki selimut ataupun permukaan bidang.
Bangun ruang sisi lengkung merupakan bangun ruang yang
punya bagian berupa lengkungan baik selimut atau permukaan bidangnya.
Jenis-Jenis Bangun Ruang Sisi
Lengkung
Tabung
Tabung adalah sebuah bangun ruang
tiga dimensi yang memiliki tutup dan alas yang berbentuk sebuah lingkaran
dengan ukuran yang sama dengan di selimuti oleh persegi panjang. Tabung juga
disebut dengan silinder.
Contoh benda berbentuk tabung yang bisa ditemui
di kehidupan sehari-hari diantaranya gelas, kaleng susu, drum, botol, seruling
dan lain sebagainya. Berikut ini gambar tabung:
Unsur-Unsur
Tabung
Berikut ini unsur atau bagian
tabung, diantaranya yaitu:
Tinggi
Tabung
Tinggi tabung adalah jarak antara bida
ng alas dan juga bidang tutup pada tabung yang biasa dinotasikan dengan menggunakan huruf t.
Jari-Jari
Tabung
Jari-jari (r) adalah jarak dari
titik pusat ke titik lain diluar bola.
Diameter
Tabung
Diameter (d) adalah jarak antara
dua titik terluar bola yang melewati titik pusat bola. Panjang diameter sama
dengan 2x panjang jari-jari.
Sisi
Tabung
Sisi
adalah kumpulan titik yang berjarak sama dengan titik pusat.
Kerucut
Kerucut adalah salah satu bangun ruang yang mempunyai sebuah alas yang berbentuk lingkaran dengan selimut yang memiliki irisan dari lingkaran.
Sisi tegak pada kerucut berupa bidang miring yang disebut selimut kerucut. Sisi lainnya disebut alas kerucut. Maka dapat disimpulkan, bahwa kerucut hanya memiliki 2 sisi, dan satu rusuk. Berikut ini gambar kerucut:
Ciri-Ciri Kerucut
Ciri-ciri kerucut diantaranya yaitu:
- Kerucut merupakan bangun ruang berbentuk limas yang alasnya berbentuk lingkaran.
- Kerucut memiliki 2 sisi.
- Kerucut memiliki 1 rusuk.
- Kerucut memiliki 1 titik puncak.
- Kerucut memiliki jaring-jaring kerucut yaitu lingkaran dan segi tiga.
Sifat-Sifat Kerucut
Berikut ini sifat-sifat kerucut, diantaranya yaitu:
- Kerucut memiliki 2 sisi (1 sisi merupakan alas yang berbentuk lingkaran dan 1 sisinya lagi berupa sisi lengkung atau selimut kerucut)
- Kerucut memiliki 1 rusuk lengkung
- Kerucut tidak memiliki rumus titik sudut.
- Kerucut memiliki 1 buah titik puncak.
- Bidang alas, yaitu sisi yang berbentuk lingkaran (daerah yang diarsir).
- Diameter bidang alas (d), yaitu ruas garis AB.
- Jari-jari bidang alas (r), yaitu garis OA dan ruas garis OB.
- Tinggi kerucut (t), yaitu jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
- Selimut kerucut, yaitu sisi kerucut yang tidak diarsir.
- Garis pelukis (s), yaitu garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.
Unsur-Unsur Kerucut
Berikut ini unsur atau bagian kerucut, diantaranya yaitu:
Bola
Bola adalah bangun ruang tiga dimensi yang dibentuk oleh titik-titik yang berjarak sama terhadap suatu titik yang disebut titik pusat bola dan bola hanya memiliki 1 sisi.
Dimensi bola dinyatakan dalam besaran jari-jari (r) atau diameter (d). Jari-jari atau radius bola adalah jarak antara permukaan bola dan titik pusat bola, sedangkan diameter bola adalah jarak garis lurus antara permukaan bola dengan permukaan sebrang titik pusat melalui titik pusat bola atau bisa dikatakan bahwa diameter bola sama dengan dua kali jari-jari bola.
Permukaan bola atau disebut juga kulit bola atau selimut bola adalah bidang yang membentuk permukaan bola. Luas permukaan bola atau disebutjuga luas kulit bola atau luas selimut bola. Gambar Bola
Unsur-Unsur Bola
Berikut ini unsur-unsur dalam bangun ruang bola, diantaranya yaitu:
Jari-Jari
Jari-jari (r) adalah jarak dari titik pusat ke titik lain diluar bola.
Diameter
Diameter (d) adalah jarak antara dua titik terluar bola yang melewati titik pusat bola. Panjang diameter sama dengan 2x panjang jari-jari.
Sisi
Sisi adalah kumpulan titik yang berjarak sama dengan titik pusat.
Titik Pusat
Titik pusat bola adalah lokasi titik inti pada ukuran bola.
Minggu, 09 September 2018
Transformasi

a) P(−2,4) terhadap sumbu x
b) Q(6,8) terhadap sumbu y
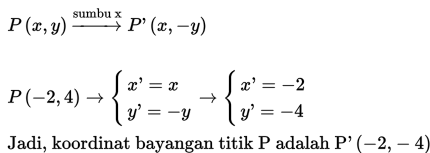
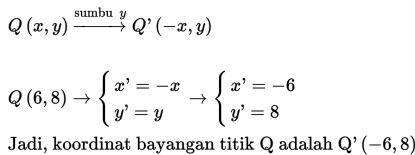
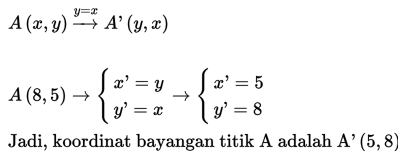
2. Translasi (pergeseran)
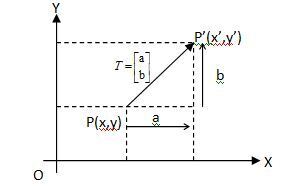
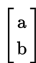
x' = x + a
y' = y + b
Translasi dapat disimpulkan sebagai berikut:
Translasi titik P(x, y) dengan menggeser absis x sejauh a dan menggeser ordinat y sejauh b,
sedemikian diperoleh titik P'(x+a, y+b), secara notasi dilambangkan:
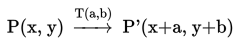
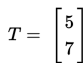
- Menentukan bayangan A:
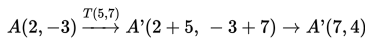
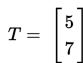
Contoh 2
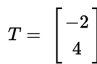
- Menentukan koordinat titik A' dan B' :
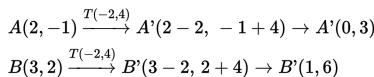
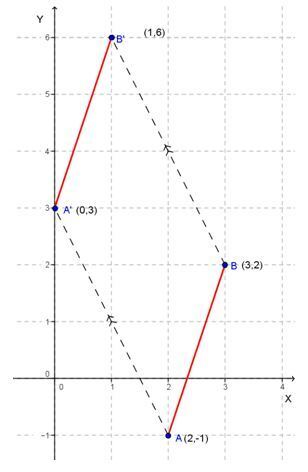
- Menggambar AB dan A'B' pada bidang kartesius:
Contoh 3
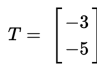
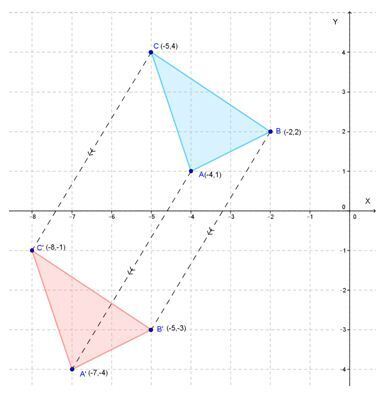
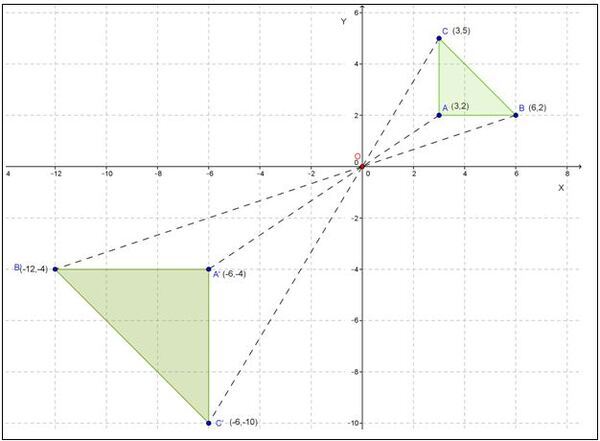
- Menentukan koordinat titik A’, B’, dan C’ :
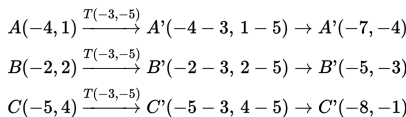
- Menggambar ∆ABC dan ∆A’B’C’ pada bidang kartesius:
Contoh 4

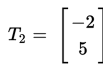
- Menentukan koordinat koordinat bayangan titik A:
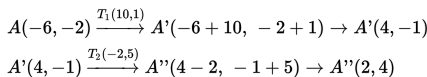

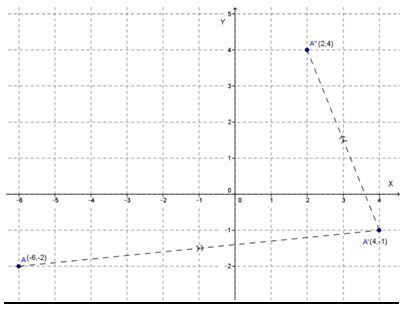
- Menggambar koordinat koordinat bayangan titik A pada bidang kartesius:
3. Rotasi(perputaran)
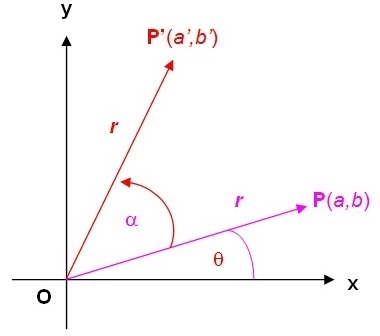


Contoh
Jawab:
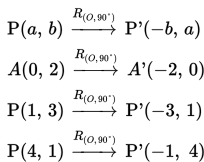
2. Mari tentukan bayangan garis y = 3x yang diputar 90° searah dengan arah perputaran jarum jam dengan pusat putar titik Q(4,2).
Jawab:
Misalkan titik P(a,b) terletak pada garis y = 3x maka b = 3a.
Bayangan titik P(a,b) adalah P’(a’,b’), dapat kamu tentukan sebagai berikut.
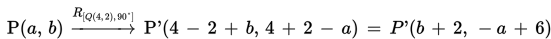
Perhatikan bahwa: a’ = b + 2 sehingga b = a’ – 2 dan b’ = -a + 6 sehingga a = -b’ + 6.
Sekarang, ayo substitusikan nilai a = -b’ + 6 dan b = a’ – 2 ke persamaan b = 3a sehingga diperoleh:
a’ – 2 = 3(-b’ + 6)
a’ – 2 = -3b’ + 18
a’ + 3b’ = 20
Jadi, bayangan garis y = 3x yang diputar 90° searah dengan arah perputaran jarum jam dengan pusat putar titik Q(4,2) adalah x + 3y = 20.
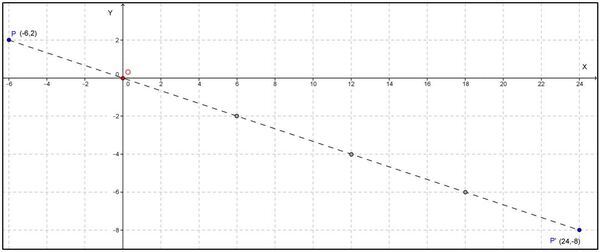
4. Dilatasi (perkalian)
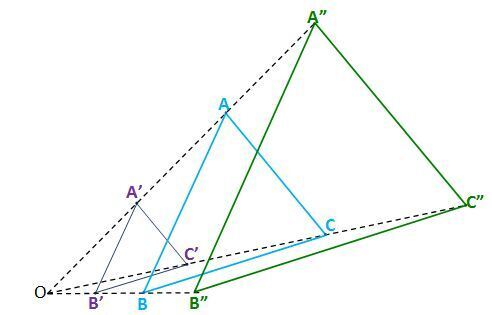
- ∆ABC diperkecil dari titik O menjadi ∆A'B'C' dengan masing-masing sisi ∆A'B'C' menjadi lebih pendek namun bentuk bangun serta ukuran sudut tetap.
- Pada gambar tersebut juga diperlihatkan bahwa ∆ABC diperbesar dari titik O menjadi ∆A"B"C" dengan masing-masing sisi ∆A"B"C" menjadi lebih panjang dan bentuk bangun serta ukuran sudut tetap.
- Pada gambar tersebut ∆A'B'C' dan ∆A”B”C” sebangun (bentuk dan ukuran sudut sama) dengan ∆ABC.

Rumus dilatasi pada bidang cartesius:
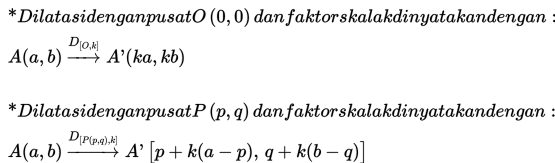
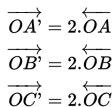

k = -4
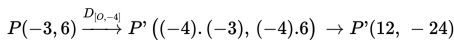
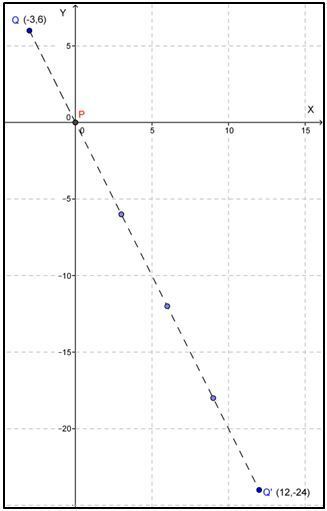
Contoh 2
Q(4,2)
k = 4
Pusat dilatasi = P(1,3)
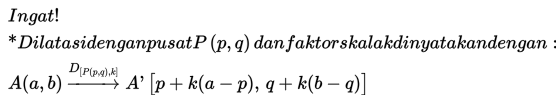
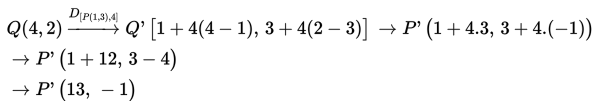
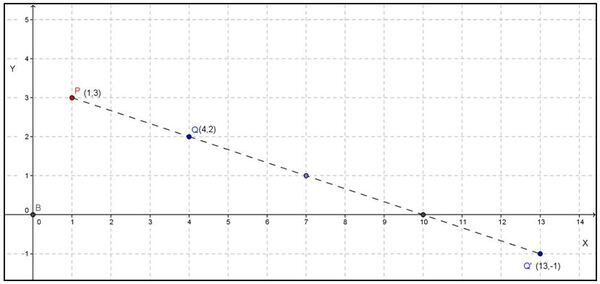
Contoh 3