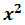PERKALIAN ALJABAR

KD 3.5 Menjelaskan bentuk aljabar dan melakukan operasi pada bentuk aljabar (penjumlahan, pengurangan, perkalian dan pembagian)

KD 4.5 Menyelesaikan masalah yang berkaitan dengan bentuk aljabar dan operasi pada bentuk aljabar

Indikator

3.5.2    Menyelesaikan operasi perkalian bentuk aljabar

4.5.2    Menyelesaikan masalah kontesktual pada operasi bentuk aljabar

Tujuan Pembelajaran

Setelah mengikuti pembelajaran siswa dapat:

  1. Menentukan hasil operasi perkalian bentuk aljabar dengan menggunakan ubin aljabar
  2. Menentukan hasil operasi perkalian bentuk aljabar dengan menggunakan sifat distributif
  3. Menentukan hasil operasi perkalian bentuk aljabar dengan cara skema
  4. Menyelesaikan masalah kontesktual pada operasi bentuk aljabar
A. Perkalian Bentuk Aljabar Menggunakan Ubin Aljabar

Contoh masalah kontekstual yang penyelesaiannya menggunakan operasi perkalian bentuk aljabar:
Pak Idris mempunyai kebun apel berbentuk persegi dan Pak Tohir mempunyai kebun jeruk berbentuk persegi panjang. Ukuran panjang kebun jeruk Pak Tohir 20 m lebih dari panjang sisi kebun apel Pak Idris. Sedangkan lebarnya, 15 m kurang dari panjang sisi kebun apel Pak Idris. Jika diketahui kedua luas kebun Pak Idris dan Pak Tohir adalah sama, maka tentukan luas kebun apel Pak Idris?
Bentuk perkalian aljabar dari masalah tersebut adalah:
Misalkan panjang sisi kebun Pa Idris x  maka luasnya 

, panjang sisi kebun Pa Tohir (π‘₯+20) , dan lebar sisi kebun Pa Tohir (π‘₯βˆ’15) , sehingga luas kebun Pa Tohir = (π‘₯+20)Γ—(π‘₯βˆ’15)  
Bentuk perkalian nya adalah yang diberi tanda kuning, bagaimana cara mengalikannya, marilah kita pelajari dulu bersama cara mengalikan dua bentuk aljabar dengan bermain ubin aljabar.
Untuk menyelesaikan perkalian dengan menggunakan ubin aljabar kita harus menyiapkan tiga bentuk ubin yang mewakili  

Berikut gambar ke tiga ubin tersebut: 


Cara menyususn ubin aljabar yaitu:
Ubin yang berdampingan dengan ubin adalah ubin x . Ubin 1 diletakkan berdampingan dengan ubin x pada bagian yang panjang sisinya 1. Bentuk gabungannya harus berbentuk persegi panjang. 

Mari kita lihat contoh soalnya dan penyelesaian dengan ubin aljabarnya.
  1. Perkalian bilangan dengan bentuk aljabar suku-2. Tentukan  hasil dari      2 Γ—(π‘₯+3) 
  2. Perkalian suku satu dengan suku-2. Tentukan hasil dari  π‘₯ Γ— ( 2π‘₯ + 3)
  3. Perkalian suku-2 dengan suku-2. Tentukan hasil dari (π‘₯+1)Γ—(2π‘₯+3)
  4. Tentukan hasil dari (π’™βˆ’πŸ)Γ—(𝒙+πŸ’)
Penyelesaian:
1. Perhatikan ubin aljabar yang sudah disusun yaitu ubin 2x + 3
 

karena dikali 2 maka ada 2 susunan ubin aljabar 2x + 3. Nah sekarang kita lihat gabungannya sebagai berikut: 

Jadi, 2Γ—(x+3)=2x+6


2. Untuk menyelesaikan π‘₯ Γ— ( 2π‘₯ + 3), perhatikan susunan ubin aljabar sebagai berikut: 

3. Untuk menyelesaikan (π‘₯+1)Γ—(2π‘₯+3), perhatikan susunan ubin aljabar sebagai berikut: 


4. 
Untuk menyelesaikan (π’™βˆ’πŸ)Γ—(𝒙+πŸ’), perhatikan susunan ubin aljabar sebagai berikut: 



Berikut adalah gambaran proses pengurangan x oleh 2 yang akan menjadi pengurangan ubin  oleh 2 ubin x dan pengurangan 4 ubin x oleh 8 ubin 1.
Berikut adalah kondisi akhir setelah proses pengurangan. 


Jadi 

Itulah cara menggunakan ubin aljabar untuk menyelesaikan perkalian bentuk aljabar.

B. Perkalian Bentuk Aljabar Menggunakan Sifat Distributif dan Cara        
    Skema




Sekarang kita telah belajar cara menyelesaikan perkalian bentuk aljabar dengan berbagai cara. nah marilah kita kembali ke permasalahan semula yaitu permasalahan menentukan luas kebun Pa Idris.

Penyelesaian masalah Pa Idris:
Pak Idris mempunyai kebun apel berbentuk persegi dan Pak Tohir mempunyai kebun jeruk berbentuk persegi panjang. Ukuran panjang kebun jeruk Pak Tohir 20 m lebih dari panjang sisi kebun apel Pak Idris. Sedangkan lebarnya, 15 m kurang dari panjang sisi kebun apel Pak Idris. Jika diketahui kedua luas kebun Pak Idris dan Pak Tohir adalah sama, maka tentukan luas kebun apel Pak Idris?
Bentuk perkalian aljabar dari masalah tersebut adalah:

C. Tugas

  1. Tentukan hasil dari (π‘₯+3)Γ—(π‘₯+2) menggunakan ubin aljabar.
  2. Tentukan hasil dari (π‘₯βˆ’5)Γ—(2π‘₯+1) dengan menggunakan sifat distributif.
  3. Tentukan hasil dari (π‘₯βˆ’3)Γ—(3π‘₯βˆ’2) dengan cara skema.
  4. Pak Badru memagari kebunnya yang berbentuk persegi panjang. Sebelum dipagari Pak Badru mengukur terlebih dahulu keliling kebunnya, dan ternyata kelilingnya adalah 180 meter. Jika selisih panjang dan lebar kebun Pak Badru adalah 10 meter, maka tentukanlah:
       a. panjang dan lebar kebun Pak Badru
       b. luas kebun Pak Badru

Materi ini bisa juga disimak penjelasan langsungnya 
Perkalian bentuk aljabar

Referensi:


Abdur Rahman As’ari, Mohammad Tohir, dkk. 2017. Buku Paket Matematika SMP/MTs Kelas VII. Kemdikbud. Jakarta: Kementerian Pendidikan dan Kebudayaan, 2017.