Pembelajaran Matematika: Maret 2020

CONTOH 1

perhatikan gambar di bawah ini

Tentukan Besar pelurus sudut SQR

PEMBAHASAN :

Dalam hal ini∠PQS dan ∠SQR merupakan sudut saling pelurus, maka:

∠PQS + ∠SQR = 180°

(5x)° + (4x+9)° = 180°

9x° + 9 = 180°

9x° = 171°

x° = 19°

Pelurus ∠SQR = ∠PQS

Pelurus ∠SQR = (5x)°

Pelurus ∠SQR = (5.19)°

Pelurus ∠SQR = 95°

CONTOH 2

Perhatikan gambar berikut

Besar sudut nomor 1 adalah 95°, dan besar sudut nomor 2 adalah 110°. Besar sudut nomor 3 adalah ….

PEMBAHASAN :

∠1 = ∠5 = 95° (sudut dalam berseberangan)

∠2 + ∠6 = 180° (saling berpelurus)

110° + ∠6 = 180°

∠6 = 70°

∠5 + ∠6 + ∠3 = 180°

95° + 70° + ∠3 = 180°

165° + ∠3 = 180°

∠3 = 15°

CONTOH 3

Perhatikan gambar di bawah ini

Besar pelurus sudut KLN adalah ….

PEMBAHASAN :

∠KLN dan ∠MLN merupakan sudut saling pelurus, maka:

∠KLN + ∠MLN = 180°

(3x + 15)° + (2x+10)° = 180°

5x° + 25° = 180°

5x° = 155°

x° = 31°

Pelurus ∠KLN = ∠MLN

Pelurus ∠KLN = (2x+10)°

Pelurus ∠KLN = (2.31 + 10)°

Pelurus ∠KLN = 72

CONTOH 4

Perhatikan gambar di bawah ini!

Tentukan besar ∠QPR?

PEMBAHASAN :

Pertama menghitung besar ∠PRQ terlebih dahulu, maka:

∠PRQ + ∠QRS = 180⁰

∠PRQ + 110⁰ = 180⁰

∠PRQ = 180⁰ - 110⁰ = 70⁰

Setelah itu hitung nilai x dalam segitiga PRQ.

Dalam segitiga terdapat jumlah ketiga sudut sebesar 180⁰.

Maka,

∠QPR + ∠PQR + ∠PRQ = 180⁰

x + x + 2⁰ + 70⁰ = 180⁰

2x + 72⁰ = 180⁰

2x = 180⁰ - 72⁰

2x = 108⁰

x = 54⁰

Besar ∠QPR = x = 54⁰

CONTOH 5

Perhatikan gambar di bawah ini

Besar penyiku ∠SQR adalah ….

PEMBAHASAN :

i∠SQR dan ∠PQS merupakan sudut saling berpenyiku, maka:

∠SQR + ∠PQS = 90°

(3x + 5)° + (6x+4)° = 90°

9x° + 9° = 90°

9x° = 81°

x° = 9°

Penyiku ∠SQR = ∠PQS

Penyiku ∠SQR = (6x+4)°

Penyiku ∠SQR = (6.9 + 4)°

Penyiku ∠SQR = 58°

CONTOH 6

Perhatikan gambar di bawah ini!

Tentukan besar pelurus sudut ABD

PEMBAHASAN :

udut berpelurus memiliki besar sudut 180⁰.

Maka,

(2x + 10)⁰ + (x + 8)⁰ = 180⁰

2x + x + 10⁰ + 8⁰ = 180⁰

3x + 18⁰ = 180⁰

3x = 180⁰ - 18⁰

3x = 162⁰

x = 54⁰

Besar sudut pelurus ABD = besar sudut CBD, sehingga:

∠CBD = x + 8⁰ = 54⁰ + 8⁰ = 62⁰

Jadi, besar sudut pelurus ABD ialah 62⁰.

CONTOH 7

erhatikan gambar

Tentukan besar ∠BCA

PEMBAHASAN :

∠ABC + ∠CBD = 180° (saling berpelurus)

∠ABC + 112° = 180°

∠ABC = 68°

∠BCA + ∠ABC + ∠BAC = 180°

∠BCA + 68° + 42° = 180°

∠BCA + 110 = 180°

∠BCA = 70°

CONTOH 8

Perhatikan gambar di bawah ini

tentukan nilai y

PEMBAHASAN :

∠CEF dan ∠EAH merupakan sudut sehadap, maka:

∠EAH = ∠CEF

∠EAH = 102°

∠EAH + ∠BAE = 180° (sudut saling berpelurus)

102°+ 3y = 180°

3y = 180° - 102°

3y = 78°

y = 26° (J

CONTOH 9

erhatikan gambar berikut!

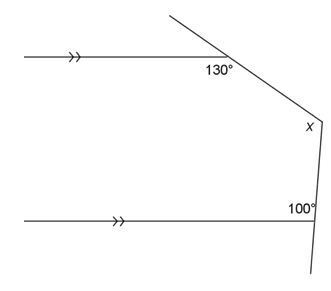
Tentukan nilai x!

PEMBAHASAN :

Buat garis bantu sejajar dua garis sejajar lainnya melalui perpotongan dua garis seperti gambar berikut.

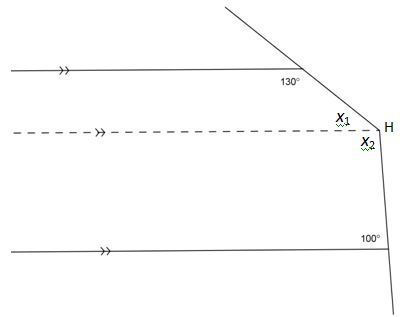
Sumber:

Soal-soal UN

Contoh 1

Diketahui panjang sebuah persegi adalah 5 cm. Maka hitungah luas dan keliling persegi tersebut!

Pembahasan:

Keliling = s + s + s + s atau 4 xs = 5 cm + 5 cm +5 cm + 5 cm = 20 cm

Luas = s x s= 5 x 5 = 25 cm²

Contoh 2

Perbandingan panjang dan lebar persegi panjang 7 : 4. Jika keliling persegi panjang tersebut 66 cm, maka luasnya adalah ….

Pembahasan:

Keliling persegi panjang adalah 66 cm, maka

$2(p + l) = 66$

$p + l = \frac{66}{2}$

$p + l = 33$

Diketahui:

$p : l = 7 : 4$

$p = \frac{7}{11} \times 33 = 21 \; cm$

$l = \frac{7]4}{11} \times 33 = 12 \; cm$

Luas persegi panjang adalah:

$L = p \times l$

$L = 21 \times 12$

$L = 252 \; cm^{2}$

Contoh 3
Diketahui keliling dari sebuah persegi yaitu 24 cm. Maka hitunglah Luas persegi tersebut!

Pembahasan:

Keliling = 4 x s

24 cm = 4 x s
s = 24 cm/4
s = 6 cm

Kemudian kita masukkan rumus luas persegi!

Luas = s x s = 6 cm x 6 cm = 36 cm²

Contoh 4

Hitunglah keliling dan luas dari persegi panjang di bawah ini!

K = p + l + p + l = 10 cm + 5 cm + 10 cm + 5 cm = 30 cm

L = p x l = 10 cm x 5 cm = 50 cm²

Contoh 5

Diketahui sebuah bangun jajargenjang memiliki alas 7 cm dan tinggi 4 cm. Tentukan luas jajargenjang tersebut!

Pembahasan:

L = a x t = 7 cm x 4 cm = 28 cm2

Contoh 6

Sebuah bangun jajargenjang mempunyai keliling 52 cm. Apabila panjang salah satu sisinya yaitu 16 cm, maka hitunglah panjang sisi yang lainnya!

Pembahasan:

Keliling = 2 x (a x t)
52 cm = 2 x (16 cm x t)
52 cm = 32 cm x 2t
52 cm – 32 cm = 2t
2t = 20
t = 20/2
t = 10 cm.

Contoh 7
anjang salah satu diagonal belah ketupat adalah 24 cm. Jika luas belah ketupat $120 \; cm^{2}$ , keliling belah ketupat adalah ….

Pembahasan:

Rumus luas belah ketupat adalah

$L = \frac{1}{2} \times d_{1} \times d_{2}$

$120 = \frac{1}{2} \times 24 \times d_{2}$

$120 = 12 d_{2}$

$d_{2} = \frac{120}{12}$

$d_{2} = 10 \; cm$

Mencari sisi belah ketupat:

$s = \sqrt{\left( \frac{1}{2} d_{1} \right)^{2} + \left( \frac{1}{2} d_{2} \right)^{2}}$

$s = \sqrt{12^{2} + 5^{2}}$

$s = \sqrt{144 + 25}$

$s = \sqrt{169}$

$s = 13 \; cm$

i keliling belah ketupat:

$K = 4s$

$K = 4 \times 13$

$K = 52 \; cm$

Contoh 8

Perhatikan bangun trapesium ABCF dan layang-layang EFCD.

Jika panjang DE = 2 cm, keliling bangun di atas adalah ….

Pembahasan:

Perhatikan ukuran lengkapnya seperti terlihat pada gambar di bawah!

Mencari OC:

$OC = \sqrt{DC^{2} - OD^{2}}$

$OC = \sqrt{17^{2} - 8^{2}}$

$OC = \sqrt{289 - 64}$

$OC = \sqrt{225}$

$OC = 15 \; \textrm{cm}$

Panjang AB = OC, sehingga keliling bangun tersebut adalah

$= 2 + 2 + 14 + 15 + 22 + 17$

$= 4 + 29 + 39$

$= 33 + 39 = 72$

Contoh 9

Perhatikan gambar!

Tentukan luas daerah yang diarsir .

Pembahasan:

ambar pada soal dapat dibagi menjadi dua yaitu persegi dan trapesium, seperti terlihat pada gambar di bawah.

Mencari tinggi trapesium:

$t = \sqrt{10^{2} - 6^{2}}$

$t = \sqrt{100 - 36}$

$t = \sqrt{64}$

$t = 8 \; \textrm{cm}$

Mencari luas persegi:

$L = s \times s$

$L = 10 \times 10$

$L = 100 \; cm^{2}$

Mencari luas trapesium:

$L = \frac{ \left( \textrm{jumlah sisi sejajar} \right) \times t }{2}$

$L = \frac{ \left( 22 + 10 \right) \times 8 }{2}$

$L = \frac{32 \times 8}{2}$

$L = 128 \; \textrm{cm}^{2}$

Jadi, luas daerah yang diarsir adalah

$L = 100 \; \textrm{cm}^{2} + 128 \; \textrm{cm}^{2}$

$L = 228 \; \textrm{cm}^{2}$

Contoh 10

Perhatikan bangun berikut!

Tentukan Keliling bangun di atas

Pembahasan:

Keliling bangun yang diberikan pada soal adalah

$= 8 \times 1 + 2 \times 1,5 + 4 \times 1,5$

$= 8 + 3 + 6$

$= 17 \; \textrm{cm}$

Contoh 11

Perhatikan gambar bangun layang-layang PQRS di bawah ini!

Apabila diketahui ∠PQR merupakan siku-siku, hitunglah luas layang-layang PQRS tersebut!

Pembahasan:

Disebabkan ∠PQR siku-siku, maka luas dari bangun layang-layang PQRS di atas bisa kita cari dengan memakai rumus luas segitiga.

Dengan alasnya = QR = 18 m serta tinggi = PQ = 13 m.

Dari layang-layang PQRS terdapat dua segitiga siku-siku yakni ΔPQR dan ΔPSR dengan luas yang sama. Oleh sebab itu luas layang-layang bisa kita cari dengan menjumlahkan dua luas segitiga siku-siku.

Luas PQRS = Luas ΔPQR + Luas ΔPSR
Luas PQRS = 2 x Luas PQR (karena luas PQR dan PSR sama)
Luas PQRS = 2 x 1/2 x 18 m x 13 m
Luas PQRS = 234 m2

Contoh 12

Perhatikan gambar di bawah ini

Tentukan keliling bangun ABCDE

Pembahasan:

encari panjang DE dengan rumus pythagoras:

$DE = \sqrt{15^{2} - 9^{2}}$

$DE = \sqrt{225 - 81}$

$DE = \sqrt{144}$

$DE = 12 \; \textrm{cm}$

Mencari keliling bangun:

$= 15 + 10 + 9 + 12 + 10$

$= 56 \; \textrm{cm}$

Contoh 13

Sebidang kebun berbentuk persegipanjang berukuran 100 m x 80 m. Di sekeliling kebun akan ditanam pohon dengan jarak 10 m antar pohon. Tentukan anyak pohon yang diperlukan
Pembahasan:

Mencari keliling persegi panjang:

$K = 2 \left( p + l \right)$

$K = 2 \left( 100 + 80 \right)$

$K = 2 \times 180$

$K = 360 \; \textrm{m}$

Mencari banyak pohon yang diperlukan:

$= \frac{360}{10}$

$= 36 \; \textrm{[pohon}$

Contoh 14
Pak Rahman mempunyai sebidang tanah berbentuk persegi panjang dengan ukuran 30 m x 25 m. Tanah tersebut dipagari kawat sebanyak tiga kali lilitan. Panjang minimal kawat yang dibutuhkan adalah ….

Pembahasan:

Mencari keliling bidang tanah yang akan dipagari kawat:

$K = 2 \left( p + l \right)$

$K = 2 \left( 30 + 25 \right)$

$K = 2 \left( 55 \right)$

$K = 110 \; \textrm{cm}$

Panjang kawat untuk mengelilingi bidang tanah sebanyak tiga kali lilitan:

$= 3 \times 110$

$= 330 \; \textrm{cm}$

Contoh 15

Pak Ali mempunyai kebun dengan bentuk seperti pada gambar di bawah.

Kebun tersebut akan dijual dengan harga Rp200.000,00 per m2. Tentukan hasil penjualan kebun Pak Ali

Pembahasan:

Gambar pada soal disusun oleh jajar genjang dan segitiga seperti terlihat pada gambar di bawah.

Mencari luas jajar genjang:

$L_{1} = a \times t$

$L_{1} = 12 \times 10$

$L_{1} = 120 \; \textrm{m}^{2}$

Mencari luas segitiga:

$L_{2} = \frac{1}{2} \times 6 \times 10$

$L_{2} = \frac{1}{2} \times 60$

$L_{2} = 30$

Jadi, luas gabungan dua bangun tersebut adalah

$L = L_{1} + L_{2}$

$L = 120 + 30$

$L = 150 \; cm^{2}$

Hasil penjualan kebun Pak Ali:

$= 150 \times Rp200.000,00$

$= Rp30.000.000,00$

Contoh 16

Perhatikan gambar!

Daerah yang diarsir adalah sketsa tanah yang ditanami rumput. Luas hamparan rumput tersebut adalah ….

Pembahasan:

uas bangun yang diberikan pada soal dapat diperoleh dari luas trapesium siku-siku dikurangi luas persegi panjang kecil, seperti terlihat pada gambar di bawah.