Pembelajaran Matematika: September 2018

Pada pembelajaran Matematika materi Transformasi Geometri meliputi Translasi (pergeseran),Refleksi (pencerminan), Rotasi (perputaran), dan dilatasi (perkalian).

1. Refleksi (pencerminan)

Refleksi merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri kearah sebuah garis atau cermin dengan jarak sama dengan dua kali jarak titik kecermin. Ada dua sifat penting dalam refleksi:

§ Jarak titik kecermin sama dengan jarak bayangan titik ke cermin.

§ Geometri yang direfleksikan berhadapan dengan petanya.

Persamaan Transformasi Pencerminan (refleksi) pada bidang

Agar lebih memahami cara menentukan titik bayangan dari hasil pencerminan, mari kita mencermati contoh soal berikut ini.

Contoh 1:

Tentukan koordinat bayangan jika direfleksikan oleh:
a) P(−2,4) terhadap sumbu x
b) Q(6,8) terhadap sumbu y

Jawab:

a) Gunakan persaman transformasi refleksi terhadap sumbu x berikut

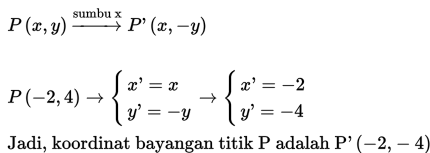
b) Gunakan persamaan transformasi refleksi terhadap sumbu y berikut

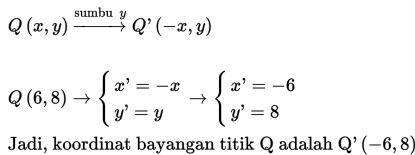
Contoh 2:

Carilah koordinat bayangannya, jika koordinat A(8,5) berikut direfleksikan terhadap garis y = x!

Jawab:

Gunakan persamaan transformasi refleksi terhadap garis y = x berikut

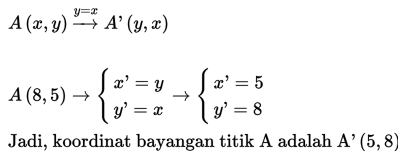
2. Translasi (pergeseran)

Translasi merupakan pergeseran atau pemindahan semua titik pada bidang geometri sejauh dan arah yang sama. Penulisan atau notasi translasi sama dengan notasi vektor. Jika titik B ditranslasi sampai titik B' maka dapat dinotasikan bB'

Contoh :

Titik A, B, dan C, masing-masing ditranslasikan ke titik A^I, B^I, dan C^I dengan jarak dan arah yang sama.

Suatu translasi dapat ditinjau terhadap sumbu x dan sumbu y. Pergeseran sejauh a

sejajar sumbu x (bergeser ke kanan a>0, ke kiri a<0) dan pergeseran sejauh b sejajar

sumbu y (bergeser ke atas b>0, ke bawah b<0) dinyatakan sebagai:

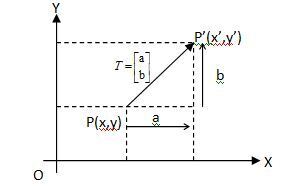
Gambar di atas memperlihatkan titik P(x,y) ditranslasi

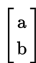
menempati P'(x',y'). Artinya P digeser ke kanan sejauh a kemudian digeser ke atas sejauh b.

Hubungan antara x, x' dengan a dan y, y' dengan b adalah sebagai berikut:
x' = x + a
y' = y + b

Translasi dapat disimpulkan sebagai berikut:

Untuk x, y, a, dan b bilangan real,
Translasi titik P(x, y) dengan menggeser absis x sejauh a dan menggeser ordinat y sejauh b,
sedemikian diperoleh titik P'(x+a, y+b), secara notasi dilambangkan:

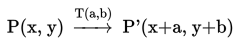
Untuk lebih jelas lagi mari kita lihat beberapa contoh soal di bawah ini:

Contoh 1:

Tentukan bayangan titik A(2,−3) terhadap translasi

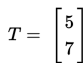
Jawab:

Menentukan bayangan A:

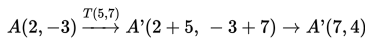
Bayangan titik A(2, 3) terhadap translasi

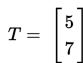
adalah A’(7, 4).

Contoh 2

Bayangan ruas garis AB terhadap translasi

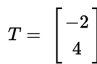
adalah A'B' . Jika koordinat titik A(2,−1) dan B(3,2) maka tentukan koordinat titik A' dan B' dan gambarkan pada bidang kartesius!

Jawab:

Menentukan koordinat titik A' dan B' :

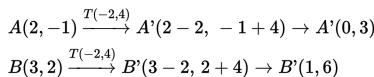
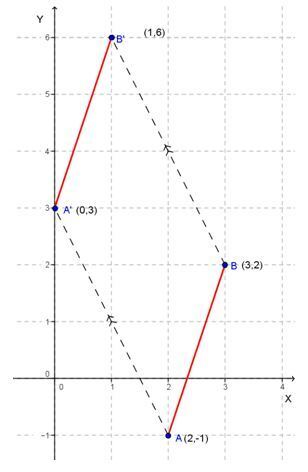
Menggambar AB dan A'B' pada bidang kartesius:

Contoh 3

Bayangan ∆ABC terhadap translasi

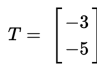
adalah ∆A’B’C’. Jika koordinat titik A(−4,1), B(−2,2), dan C(−5,4) maka tentukan koordinat titik A’, B’, C’ dan gambarkan pada bidang kartesius!

Jawab:

Menentukan koordinat titik A’, B’, dan C’ :

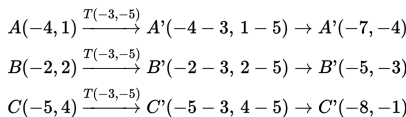
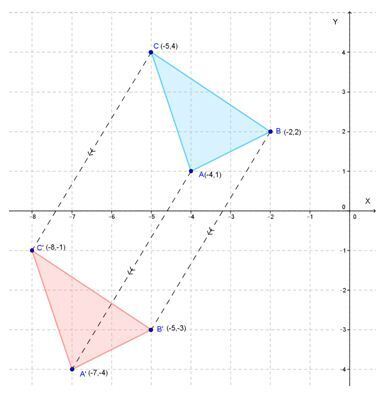
Menggambar ∆ABC dan ∆A’B’C’ pada bidang kartesius:

Contoh 4

Titik A(−6,−2) ditranslasikan terhadap translasi

kemudian ditranslasikan lagi

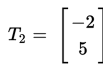
maka tentukan koordinat bayangan titik A dan gambarlah pada bidang kartesisus!

Jawab:

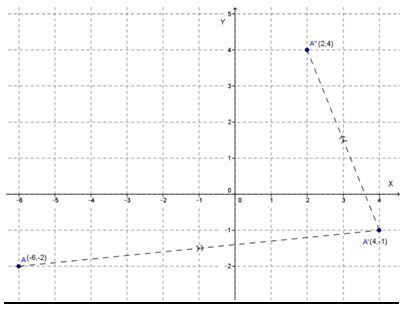
Menentukan koordinat koordinat bayangan titik A:

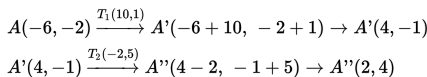
Bayangan A(−6,−2) terhadap translasi

adalah A"(2,4).

Menggambar koordinat koordinat bayangan titik A pada bidang kartesius:

3. Rotasi(perputaran)

Rotasi atau perputaran merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri sepanjang busur lingkaran yang memiliki titik pusat lingkaran sebagai titik rotasi. Rotasi dinyatakan positif jika arahnya berlawanan jarum jam, dan bernilai negatif jika searah jarum jam. Sebagai contoh:

Misalkan, posisi awal pensil jangka pada titik P(a,b). Setelah dirotasi sebesar α dengan pusat titik O, posisi pensil jangka ini berada pada titik P’(a’,b’) seperti pada gambar berikut.

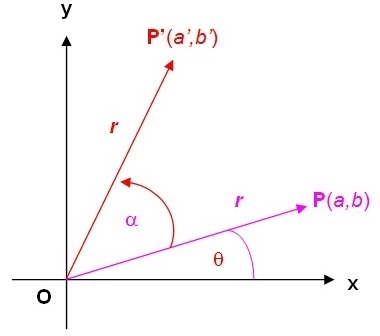
Rotasi dengan titik pusat O(0,0)

Rotasi dengan titik pusat S(m,n)

Contoh

1. tentukan bayangan segitiga ABC dengan titik sudut A(0,2), B(1,3), dan C(4,1) yang diputar 90° berlawanan dengan arah perputaran jarum jam dengan pusat putar titik O(0,0).
Jawab:

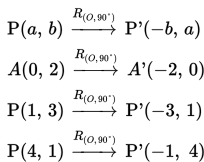
Jadi, bayangan segitiga ABC tersebut jika diputar 90° berlawanan dengan arah perputaran jarum jam dengan pusat putar titik O(0,0) adalah segitiga A’B’C’ dengan A’(-2,0), B’(-3,1), dan C’(-1,4).
2. Mari tentukan bayangan garis y = 3x yang diputar 90° searah dengan arah perputaran jarum jam dengan pusat putar titik Q(4,2).
Jawab:
Misalkan titik P(a,b) terletak pada garis y = 3x maka b = 3a.
Bayangan titik P(a,b) adalah P’(a’,b’), dapat kamu tentukan sebagai berikut.

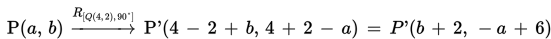
Jadi, titik P’(b + 2,-a + 6).
Perhatikan bahwa: a’ = b + 2 sehingga b = a’ – 2 dan b’ = -a + 6 sehingga a = -b’ + 6.
Sekarang, ayo substitusikan nilai a = -b’ + 6 dan b = a’ – 2 ke persamaan b = 3a sehingga diperoleh:
a’ – 2 = 3(-b’ + 6)
a’ – 2 = -3b’ + 18
a’ + 3b’ = 20
Jadi, bayangan garis y = 3x yang diputar 90° searah dengan arah perputaran jarum jam dengan pusat putar titik Q(4,2) adalah x + 3y = 20.

4. Dilatasi (perkalian)

Dilatasi merupakan transformasi geometri berupa perkalian yang memperbesar atau memperkecil suatu bangunan geometri. Dalam konsep dilatasi, ada yang disebut titik dilatasi dan faktor dilatasi.

Titik dilatasi merupakan titik yang menentukan posisi suatu dilatasi. Titik dilatasi menjadi titik pertemuan dari semua garis lurus menghubungkan antara titik-titik dalam suatu bangun ketitik-titik hasil dilatasi.

Faktor dilatasi merupakan faktor perkalian suatu bangun geometri yang didilatasikan. Faktor ini menunjukan seberapa besar hasil dilatasi terhadap bangun geometrinya dan dinotasikan dengan k. Nilai k > 1 atau k < -1 menunjukan hasil dilatasi lebih besar dari geometrinya. Nilai -1 < k < 1 menunjukan hasil dilatasi lebih kecil dari geometrinya. Tanda positif mengartikan geometri dan hasil dilatasi berdampingan di salah satu sisi titik dilatasi. Sedangkan tanda negatif mengartikan geometri dan hasil dilatasi saling terbalik dan berlainan sisi di titik dilatasi.

Dilatasi dapat ditulis:(D, k) = (Titik dilatasi, faktor dilatasi)Adalah transformasi yang mengubah ukuran bangun tetapi tidak mengubah bentuknya

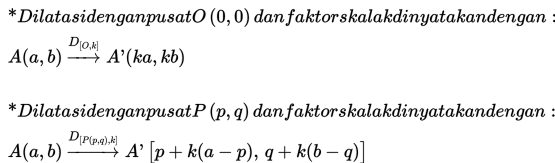
diketahui ukuran bangun sebelum didilatasi dan setelah didilatasi.

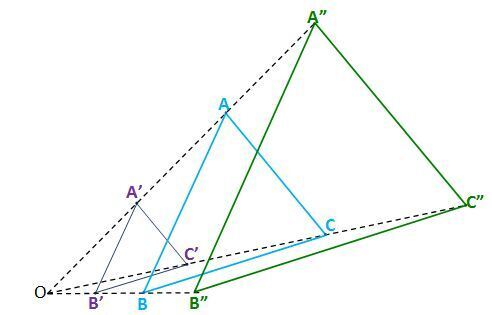
Pada gambar di atas, kalian dapat melihat bahwa:

∆ABC diperkecil dari titik O menjadi ∆A'B'C' dengan masing-masing sisi ∆A'B'C' menjadi lebih pendek namun bentuk bangun serta ukuran sudut tetap.
Pada gambar tersebut juga diperlihatkan bahwa ∆ABC diperbesar dari titik O menjadi ∆A"B"C" dengan masing-masing sisi ∆A"B"C" menjadi lebih panjang dan bentuk bangun serta ukuran sudut tetap.
Pada gambar tersebut ∆A'B'C' dan ∆A”B”C” sebangun (bentuk dan ukuran sudut sama) dengan ∆ABC.

Perubahan ukuran tanpa merubah kesebangunan itulah yang nantinya kita kenal sebagai dilatasi. Dilatasi membutuhkan titik pusat dan k faktor skala. Nilai faktor skala (k) inilah yang nantinya akan menentukan apakah dilatasi merubah ukuran bangun menjadi lebih kecil atau menjadi lebih besar dari sebelumnya.

Rumus dilatasi pada bidang cartesius:

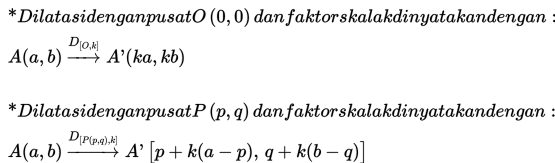
ontoh Dilatasi (dengan faktor skala k < -1)

Terdapat ∆ABC yang didilatasi dengan faktor skala k = −2 dengan pusat O(0,0);

Karena skala bernilai negatif, maka arah garis berlawanan.

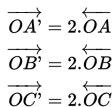
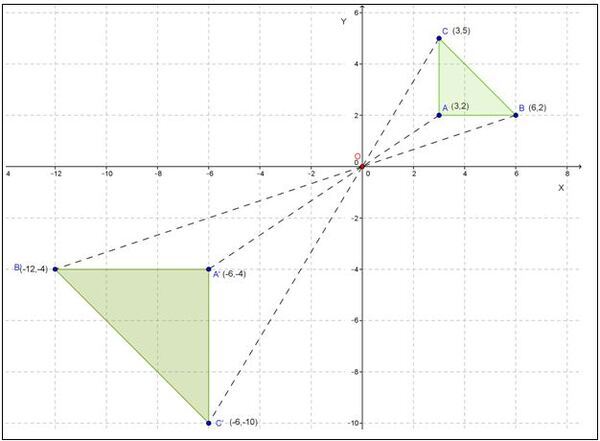
Dari gambar di atas dapat kalian lihat ∆ABC pada bidang cartesius tersebut, koordinat titik A(3,2), B(6,2), dan C(3,5) didilatasi dari titik O(0,0) dengan skala k = −2. Hasil dilatasi berupa ∆A'B'C'.

Contoh 1

Tentukan koordinat bayangan titik P(-3,6) pada didilatasi dengan pusat O(0,0) dengan faktor skala −4 !

Jawab:

P(−3,6)
k = -4

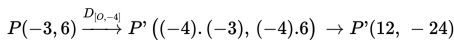
Apabila digambarkan dalam koordinat kartesius:

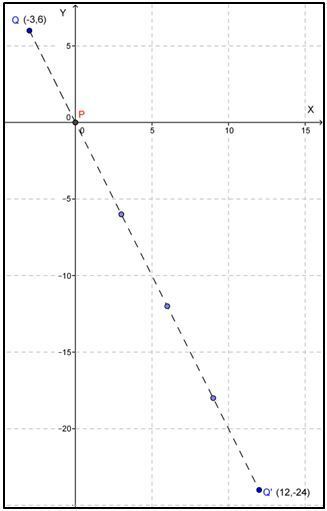
Jadi, koordinat bayangan titik P(−3,6) pada didilatasi dengan pusat O(0,0) dengan faktor skala −4 adalah P’(12,−24).

Contoh 2

Tentukan koordinat bayangan titik Q(4,2) pada didilatasi dengan pusat P(1,3) dengan faktor skala 4 !

Jawab:

Q(4,2)
k = 4
Pusat dilatasi = P(1,3)

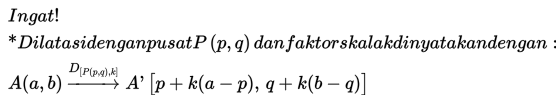
Dengan demikian, dapat diperoleh:

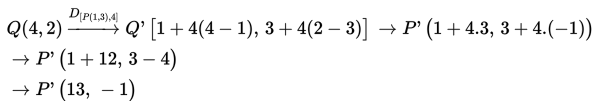
Apabila digambarkan pada koordinat kartesius:

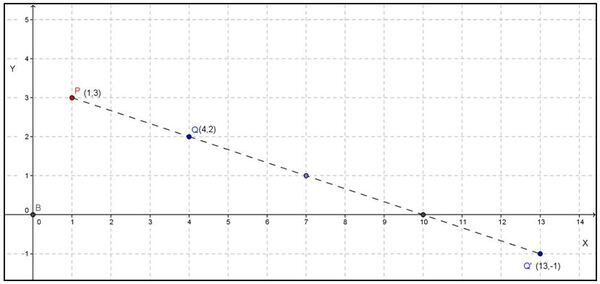
Koordinat bayangan titik Q(4,2) pada didilatasi dengan pusat P(1,3) dengan faktor skala 4 adalah Q’(13,−1)

Contoh 3

Bayangan titik P(−6,2) pada dilatasi [O,k] adalah P’(24,−8) maka tentukan nilai k !

Jawab:

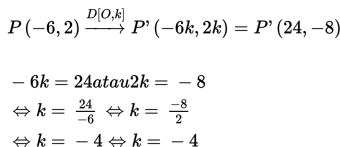
Apabila digambarkan pada koordinat kartesius:

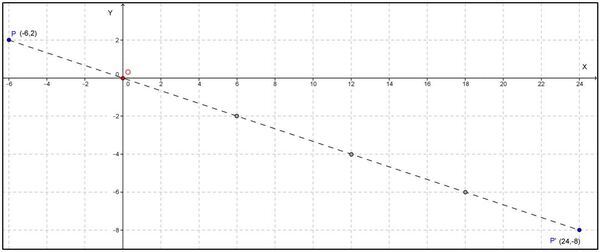
Jadi, faktor skala k = −4

Sebagai gambaran umum tentang transformasi geometri dapat kalian lihat video berikut ini :

Semoga bermanfaat,,,

Sumber Buku paket karangan Subchan, M.Sc, Ph.D ,dkk. Buku Siswa Matematika SMP/Mts kls XI. Jakarta: Pusat Kurikulum dan Perbukuan, Balitbang, Kemdikbud

Quizizz merupakan sebuah web tool untuk membuat permainan kuis interaktif untuk digunakan dalam pembelajaran di kelas anda misalnya saja untuk penilaian formatif. Penggunaannya sangat mudah, kuis interaktif yang anda buat memiliki hingga 4 pilihan jawaban termasuk jawaban yang benar. Anda juga dapat menambahkan gambar ke latar belakang pertanyaan dan menyesuaikan pengaturan pertanyaan sesuai keinginan anda. Bila kuis anda sudah jadi, anda dapat membagikannya kepada siswa anda dengan menggunakan kode 5 digit yang dihasilkan.

Quizizz juga memberikan data dan statistik tentang kinerja siswa anda. Anda dapat melacak berapa banyak siswa yang menjawab pertanyaan yang anda buat, pertanyaan yang harus dijawab dan banyak lagi. Anda bahkan bisa mendownload statistik ini dalam bentuk spreadsheet Excel. Fitur "pekerjaan rumah" juga tambahan fitur yang menarik. Pekerjaan rumah memungkinkan anda menetapkan kuis sebagai pekerjaan rumah, dan membatasi waktu pengerjaan pekerjaan rumah tersebut hingga 2 minggu. Dengan Quizizz, siswa bisa bermain kapan saja dan dari mana saja.Melalui pelatihan online Samisanov kali ini peserta akan dijabarkan mulai dari instalasi aplikasi sampai kepada pembuatan Soal menjadi aplikasi yang baru dan siap untuk di gunakan.

Pelaksanaan Pelatihan Membuat Kuis dengan Quizziz dilaksanakan tanggal 24 Agustus - 8 September 2018

Terimakasih atas share ilmunya Pak Ardi Kusnadi, terimakasih IGI….

Terima kasih pada Bapak Endang Iwan, S.Pd, M.M selaku kepala sekolah SMPN 46 Bandung yang telah memberikan izin untuk mengikuti pelatihan ini

Terimakasih siswa-siswi kelas 9C SMP Negeri 46 Bandung yang telah bermain game bersama ibu…